主成分分析（PCA）とは？機械学習での活用例や固有値などについて解説

最終更新日:2023/09/28

主成分分析（PCA）は、多変数データの情報を要約し、その本質を捉えるための強力な手法です。

分散が最大となる方向を見つけ出し、それを新たな軸としてデータを変換します。これにより、データの次元を減らすことが可能となり、データの解釈が容易になります。

この記事では、下記について分かりやすく解説します。

• PCAの基本的な計算方法
• 固有値などの重要指標の解説
• 実際のデータ解析における活用例

また、PCAと因子分析の違いについても触れ、どのような条件下でどちらの手法を選択すべきかについても説明します。

テキストマイニングについて詳しく知りたい方は以下の記事もご覧ください。
テキストマイニングの目的や活用方法｜ツールを使うメリットや注意点・選び方を紹介します！

主成分分析（PCA）とは

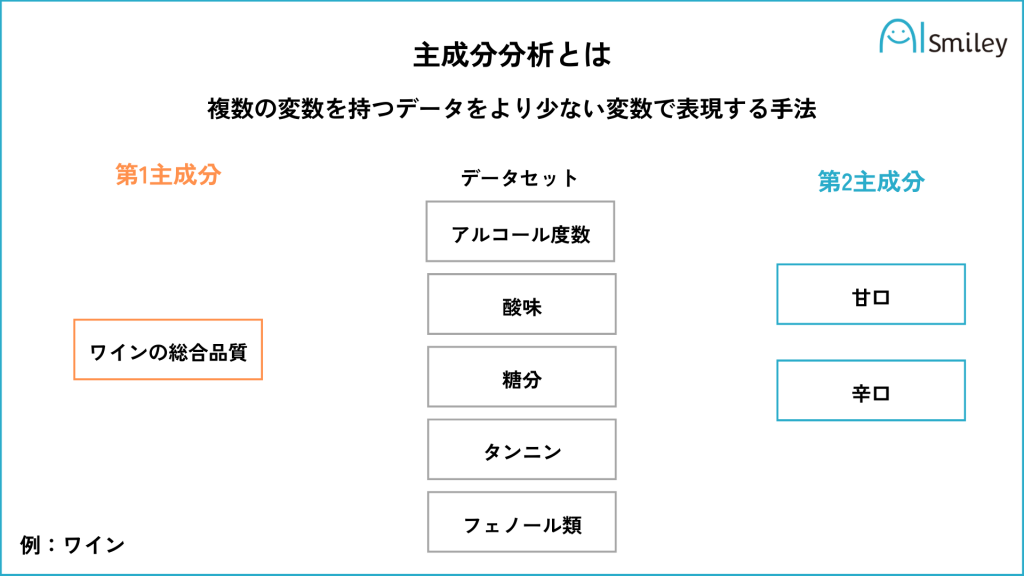
主成分分析（PCA）は、多次元データの情報を損なわずに低次元空間に縮約する統計的な解析手法です。

具体的には、複数の説明変数を、より少ない指標や合成変数に要約します。この要約は「次元の縮約」とも呼ばれます。

主成分分析によって分かること

主成分分析を理解するためには、様々な重要指標を知る必要があります。
それぞれ例を交えて分かりやすく解説します。

①固有値、寄与率、累積寄与率

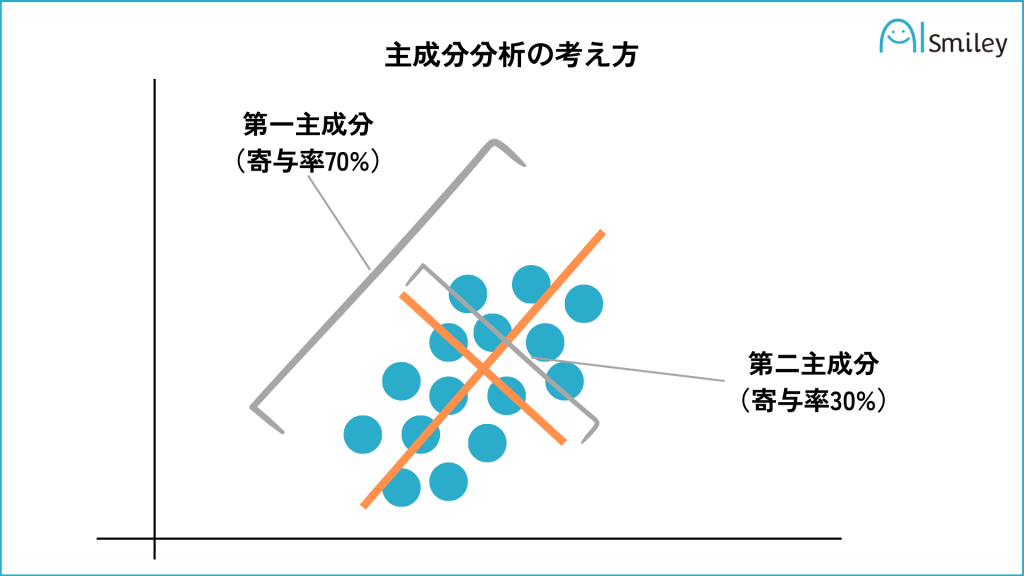
主成分分析の結果を理解するためには、「固有値」、「寄与率」、「累積寄与率」の3つの概念を把握することが重要です。これらは主成分分析の成果を評価し、適切に解釈するための基礎知識です。

それぞれわかりやすく解説します。

固有値
まず、「固有値」についてです。固有値は、各主成分が元のデータをどれだけ説明できるかを表す指標です。具体的には、各主成分が持つ情報の量や重要度を表します。固有値が大きいほど、その主成分は元のデータをよく表現していると言えます。

例えば、野菜を評価するためのデータがあり、色や形、大きさ、味などの多くの変数を持つとします。これらの変数を主成分分析にかけると、「色と形が似ている野菜」や「大きさと味が関連する野菜」など、新たな指標（主成分）が生まれます。この新たな指標のそれぞれが、元のデータをどれだけ説明できるかが固有値です。

寄与率
次に、「寄与率」について説明します。寄与率は固有値を全ての固有値の合計で割ったもので、その主成分が元のデータ全体のうちどれだけを説明できるかをパーセンテージで表します。寄与率が高いほど、その主成分は元のデータの情報を多く含んでいると言えます。

先程の野菜の例で言うと、全ての野菜に関する情報（色、形、大きさ、味）の中で、「色と形が似ている野菜」や「大きさと味が関連する野菜」がそれぞれ何%を占めるかを示す指標が寄与率です。

累積寄与率
最後に、「累積寄与率」について説明します。累積寄与率は、選択した主成分までの寄与率の合計を示します。これにより、選んだ主成分が元のデータの全情報のうちどれだけを説明できるかを知ることができます。通常、累積寄与率が70%~80%を超える点までの主成分を選択すると良いとされています。

引き続き野菜の例を使用すると、たとえば第1主成分（「色と形が似ている野菜」）の寄与率が40%、第2主成分（「大きさと味が関連する野菜」）の寄与率が30%だったとします。この場合、これら2つの主成分を合わせて考慮すると、全体の情報の70%（40% + 30%）を説明できることになり、十分な情報を得られると言えます。この70%が累積寄与率です。

それぞれが主成分分析における重要な指標であり、これらを用いてデータ解析を進めることが、主成分分析の成功につながります。また、これらの概念を理解することで、データの背後にある構造や傾向をより深く探ることが可能となります。

② 主成分負荷量

主成分分析の結果を解釈する際に重要な指標の一つが、主成分負荷量です。主成分負荷量は、各変数が新たに抽出された主成分にどれだけ寄与しているのかを数値で示します。この値が大きいほど、その変数は主成分の形成に大きく寄与していると言えます。また、この値はマイナスになることもあります。マイナスの場合、その変数が主成分と逆の関係性を持っていることを示します。

これを理解するために、再び野菜の例を挙げましょう。野菜の形状、色、大きさ、甘さといった特徴を変数として、それぞれの主成分負荷量を調べます。もし第1主成分の負荷量が形状が0.8、色が0.7で、他の変数の負荷量が全て0.3以下だった場合、この第1主成分は「色と形状が類似する野菜」を表していると解釈できます。

次に、これらの負荷量をテーブルで表現します。変数と第1主成分の負荷量の関係を以下のように表すことができます。

変数	主成分負荷量
形状	0.8
色	0.7
大きさ	0.2
甘さ	0.3

主成分分析における主成分負荷量の理解は、抽出された主成分が元の変数とどのような関係を持つのかを理解する上で重要です。また、主成分負荷量は、主成分が元のデータのどの部分を強調して表現しているのかを示しているため、データ解析の結果を解釈する際には必要不可欠な指標となります。

③主成分得点

主成分分析における「主成分得点」は、個々のデータが新たに作成された主成分上でどの位置にあるのかを示すスコアのことを指します。主成分得点は、各主成分を新たな座標軸と見なしたときのデータの座標値とも言えます。つまり、これらの得点によって元の多次元データを低次元で表現することが可能となります。

野菜の例を用いて説明しましょう。各野菜（データ）が持つ色、形、大きさ、甘さ（変数）を元に主成分分析を行い、第一主成分と第二主成分を抽出します。これらの主成分は新たな座標軸となり、各野菜はこの座標上の位置（主成分得点）によって表現されます。例えば、カボチャは色と形の得点が高く、大きさと甘さの得点が低いかもしれません。

主成分得点は、元のデータを主成分上にプロットする際の座標となります。これを以下のようなテーブルにすると以下のようになります。

野菜	第一主成分得点	第二主成分得点
トマト	0.5	-0.3
かぼちゃ	0.8	-0.2
ピーマン	-0.6	0.7

主成分得点は、各データがどの主成分を強く持つのか、または弱く持つのかを示すため、データの特性を理解するのに非常に有用です。

また、主成分得点を元にデータを2次元の平面上にプロットすることで、データ間の関係性を視覚的に理解することも可能です。これらの理解により、データの背後にある構造やパターンをより深く理解することができます。

主成分分析のメリットと活用法

①情報を集約しながら変数を減らすことができる

主成分分析の最大のメリットは、情報の集約と変数の減少が可能であることです。
多変数のデータを、情報を損なわずに少数の変数で表現することができます。

②データのグラフ化が可能となる

主成分分析により、多次元データを2次元や3次元のグラフに描画できます。これにより、データの全体像を視覚的に理解しやすくなります。

③変数間の関係性を知ることができる

主成分分析を用いると、多数の変数間の相関関係を調査することが可能となります。変数間の強弱関係を可視化することで、データの特性をより深く理解することができます。

主成分分析の注意点

①各主成分の持つ意味は分からない

主成分分析は数学的な手法によって新たな指標（主成分）を作り出しますが、それぞれの主成分が具体的に何を表しているのかという意味は分からないことが多いです。そのため、解釈の際には注意が必要です。

②寄与率が低すぎて役に立たないこともある

主成分分析において、寄与率が低すぎるとその主成分は全体の分散をほとんど説明できないため、その主成分を利用する意味が薄れます。適切な主成分の選択が求められます。

主成分分析の活用例

主成分分析はそのユニバーサルな性質から、多様な分野で活用されています。ここでは、具体的な活用例としてマーケティングとテスト結果の分析を取り上げます。

例①マーケティング（顧客の分類）

マーケティングにおいては、顧客の行動や好みを理解することが非常に重要です。

たとえば、顧客が好む商品の種類、購入する日時、好む広告のスタイルなど、多くの異なる変数を考慮に入れる必要があります。主成分分析は、これら多数の変数から、最も重要な情報を抽出して新たな変数（主成分）を作り出すのに役立ちます。

データ収集：顧客の購買履歴やアンケート結果などから多次元データを集めます。
主成分分析：収集したデータに主成分分析を適用し、主成分を抽出します。
顧客分類：抽出した主成分に基づき、顧客を分類します。

この結果、新たな顧客セグメントを発見することができるかもしれません。例えば、特定の広告スタイルを好む顧客、週末に主に購入する顧客、特定の商品カテゴリーを好む顧客など、様々な視点で顧客の行動を理解することが可能となります。

例②テスト結果の分析

また、主成分分析はテスト結果の分析にも活用されます。学生のテストの成績には多くの変数が存在します。例えば、数学の成績、英語の成績、理科の成績、体育の成績などです。これらの変数から主成分分析を用いて学生の能力の特徴を抽出することができます。

データ収集：各学生の各教科の成績を集めます。
主成分分析：収集した成績データに主成分分析を適用し、主成分を抽出します。
成績解釈：抽出した主成分に基づき、各学生の成績の傾向や特徴を理解します。

例えば、文理の才能が同時に高い学生、あるいは特定の科目に特化した学生など、新たな視点で学生の成績を解釈することが可能となります。これにより、個々の学生に対するより適切な教育支援を計画することができます。

以上のように、主成分分析は多次元データから主要な情報を抽出する手法として、マーケティングや教育など、さまざまな分野で活用されています。異なる状況や目的に合わせて、この有用な手法を使いこなすことで、より良い解析結果や洞察を得ることが可能です。

主成分分析とAI製品

主成分分析はAI製品を活用することで、より効率的に分析することができます。

AI製品を用いた主成分分析の手順

AI製品を利用すると、主成分分析の手順を自動化でき、高速に解析を進めることができます。一般的な手順は、まず元のデータをAI製品にインプットし、次にデータの前処理を行います。前処理とは、欠損値の補完や変数の正規化などを指します。その後、主成分分析を実行し、結果を解釈するという流れになります。

AI製品を用いた主成分分析のメリット

AI製品を使用することで、主成分分析の時間と労力を大幅に削減することができます。また、自動化により分析の再現性が向上し、誤りの可能性も低減します。

おすすめのAI製品とその特徴

AI製品としては、「RapidMiner」や「Orange」などがあります。これらはビジュアルインターフェースを備えているため、コードを書くことなく主成分分析を行うことができます。また、分析結果の可視化機能も充実しており、データ解析を直感的に行うことができます。

主成分分析のアルゴリズム

主成分分析のアルゴリズムは、以下の手順で進行します。

1. データの標準化: 各変数の平均を0、標準偏差を1にする
2. 共分散行列の作成: 各変数間の共分散を計算する
3. 共分散行列の固有値と固有ベクトルの計算: 最大の固有値を持つ固有ベクトルが第一主成分となる
4. 固有ベクトルを用いたデータの変換: 元のデータを固有ベクトルに投影することで、新しいデータ（主成分得点）を作成する

この手順を通じて、主成分分析はデータを新たな座標系に変換します。

主成分分析と因子分析の違い

主成分分析と因子分析はどちらも次元削減の手法ですが、その目的とアプローチに違いがあります。主成分分析はデータの全体的な構造を把握するために使用され、変数間の相関を最大化する新たな軸（主成分）を見つけ出します。

一方、因子分析は潜在的な構造を見つけ出すために使用され、観測データの背後に存在する共通の要素（因子）を見つけ出すことを目指します。

主成分分析と因子分析の主な違いは以下の通りです。

	主成分分析	因子分析
目的	データの全体的な構造を把握	潜在的な構造を見つけ出す
方法	変数間の相関を最大化する軸を見つける	共通の要素（因子）を見つけ出す
解釈	抽出された主成分の意味付けは困難	因子に対して具体的な意味付けが可能

主成分分析をPythonで行う方法

Pythonのscikit-learnライブラリを用いると、簡単に主成分分析を行うことができます。以下に簡単なコードを示します。

from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler

# データの標準化
sc = StandardScaler()
X_std = sc.fit_transform(X) # Xは元のデータ

# 主成分分析の実行
pca = PCA(n_components=2) # 主成分の数を指定
X_pca = pca.fit_transform(X_std)

上記のコードでは、まずデータを標準化し、その後に主成分分析を行っています。ここでは2つの主成分を抽出していますが、必要に応じて主成分の数を変更することが可能です。

まとめ

主成分分析は、多変量データを理解しやすいように、情報を失わない範囲で次元削減を行う強力な分析手法です。データの背後にある関係性を理解し、無駄な変数を取り除くことで、効果的な分析とデータ解釈が可能となります。

しかし、主成分分析を適用する前に、データの特性や要件を十分に理解することが必要で、各主成分が何を示しているのか、どの程度の寄与率を持つのかなど、解釈には注意が必要です。また、Pythonなどのプログラミング言語や、AI製品を活用することで、主成分分析の手法はさらに進化し、活用の幅が広がります。

因子分析とは異なるアプローチであることも理解し、適切な分析手法を選択することで、データからより深い洞察を引き出すことが可能となります。

データマイニングについて詳しく知りたい方は以下の記事もご覧ください。
データマイニングとは？手法・活用例・AIツールを使ったやり方をご紹介

データ分析について詳しく知りたい方は以下の記事もご覧ください。
データ分析とは？基礎から分かる手法と流れ、仕事でのメリットも解説

AIについて詳しく知りたい方はこちらの記事もご覧ください。
AI・人工知能とは？定義・歴史・種類・仕組みから事例まで徹底解説

よくある質問

主成分分析と因子分析の違いは何ですか？

主成分分析と因子分析の両者は多変量データの次元削減を目的とした方法ですが、アプローチに違いがあります。主成分分析はデータの分散を最大化する軸を見つけるのに対し、因子分析はデータの背後に存在する潜在的な要素や構造を見つけ出すための方法です。

主成分分析の結果はどのように解釈すればいいのでしょうか？

主成分分析の結果は、それぞれの主成分がデータのどの部分を表しているかを理解することが重要です。また、それぞれの主成分の寄与率を確認し、どの主成分がデータ全体の分散をどの程度説明しているかを理解します。しかし、各主成分が何を示すのかは一概には言えませんので、注意が必要です。

主成分分析のメリットとデメリットは何ですか？

主成分分析のメリットは、多次元データを低次元に削減しながら、データのバリエーションを最大限に保つことができる点です。また、データのパターンや構造を視覚的に表現しやすくなるのも大きな利点です。デメリットとしては、主成分の解釈が難しいこと、また、全ての情報を保持するわけではないため、重要な情報が失われる可能性もあります。

主成分分析はどのような場面で使われますか？

主成分分析は、マーケティングで顧客の分類、製品のポジショニング、また医療や生物学での研究など、多変量データが存在し、その特性を理解する必要がある場面で広く使われます。また、機械学習の前処理としても利用され、高次元データの次元削減を行うことで、計算量を減らす効果があります。 主成分分析は広範な分野で活用されており、その有用性はますます高まっています。データ解析を進める上で、主成分分析は欠かすことのできない重要な手法であると言えるでしょう。