決定木分析とは？回帰分析との違いや活用の方法をわかりやすく解説

最終更新日:2024/05/22

決定分析とは？

仕事でデータ分析をよく行わなければならない人の場合、分析をするために覚えなければならない手法の種類が多く、最適な手法を選択するのに初心者ほど迷ってしまう傾向にあります。

分析手法を都度迷わずに一定の基準に照らして選択できるようになるためには、1つ1つの分析手法の特徴を理解しておく必要があります。

この記事では、データ分析をする際の手法の1つである決定木分析の内容から活用方法まで詳しく解説します。

決定木分析(ディシジョンツリー)とは？見方や回帰分析との違い

決定木分析とは、データを基に決定木（読み方＝けっていぎ）と呼ばれる樹形図（問題を枝分かれさせてどんな組み合わせがあるかを見やすく示し、原因や解決策を論理的に探すために作成する図）を作成し、分析を行う方法のことで英語では「decision tree analytics」と言います。

決定木の具体的な例、回帰分析と決定木分析の違い、決定木分析の見方、決定木分析の活用シーンの4つの観点から決定木分析をさらに詳しく紹介します。

決定木は予測の目的や達成したい予測の精度に応じて次のような種類に分類できます。

決定木分析をする目的が、数値ではないものの予測の場合は分類木、数値の予測の場合は回帰木を使う、と覚えれば理解しやすいです。

一方1つの決定木を用いて決定木分析をするだけでは予測の精度が低く、課題の解決につながるような分析ができない場合に用いられるのがアンサンブル学習やランダムフォレストです。

決定木は目的に応じて使い分けができ、組み合わせ方を変えることで複雑な分析にも対応できると認識しておくのが大切です。

回帰分析と決定木分析の違い

回帰分析とは、物事の原因となっている変数の「説明変数」と物事の結果となっている変数の「目的変数」の関係性を調べるのを目的として、データを関数に当てはめて分析する方法のことです。

具体的には、目的変数yの変動は説明変数xの変動とどのように関係し、影響しているかを分析します。

目的変数と説明変数の関係を数式で表したものを「回帰式」と呼びます。

回帰分析には次の2種類があります。

回帰分析と決定木分析では、どちらも目的変数を予測するのを目的としている点が共通しています。

しかし、回帰分析が回帰式を使って目的変数を予測するのに対し、決定木分析では樹形図の分岐で目的変数を予測するという違いがあります。

また回帰分析の結果は数値ですが、決定木分析の結果は樹形図です。

これらのことから、回帰分析と決定木分析は変数の予測方法や得たい結果の形式によって使い分けが必要だと言えます。

決定木分析の見方

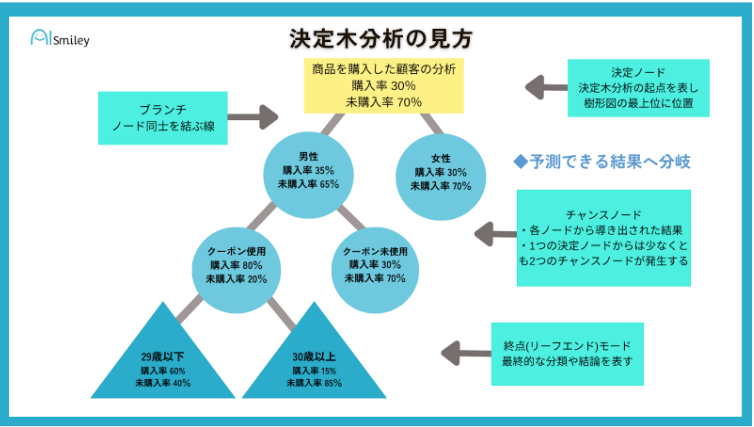
決定木分析においては、樹形図で予測できる全ての選択を行った場合の結果を可視化することでデータの分析を行います。

決定木分析の結果を見る際に覚えておきたい樹形図内の各箇所の名称は次の通りです。

決定木は通常1つの決定ノードから始まり、予測できる結果へと分岐していくという全体像がイメージできると、決定木分析の結果を理解しやすくなります。

決定木分析の活用シーン

決定木分析はマーケティングの分野、金融の分野、医療の分野など分析を必要とするシーンでさまざまに活用されていますが、マーケティング分野における活用シーンを例として2つご紹介します。

顧客満足度につながる要因を特定する

顧客満足度の向上が企業の商品やサービスを購入してもらう上で重要なのはわかっていても、「どのような要因が顧客満足度を高めているのか」まで、分析できていない企業も多いと思われます。

顧客に対してアンケート調査を行い、そのデータを基に決定木分析を行ってみると顧客満足度につながる要因を特定できます。

例えばアンケートの内容から決定ノードを「クーポンの使用」とし、Yesのブランチでつないだチャンスノードには「クーポンを複数回利用」Noでつないだチャンスノードには「クーポンの存在は知っていた」といった形でパターン分けをして記載します。

アンケートの結果を、チャンスノードをいくつか経て終点ノードまで書き込むことができれば、クーポンの使用が顧客満足度にどのようにつながっているのかが明らかになります。

購入率の高いターゲットを特定する

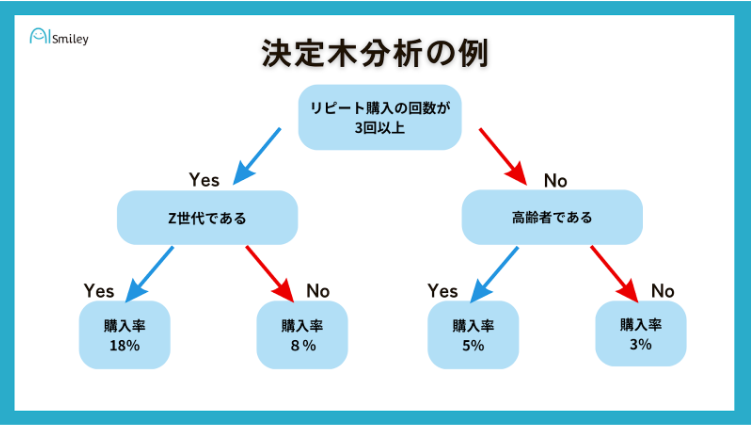
企業が購入率の高いターゲット顧客のペルソナ像が特定できれば、そのペルソナに合った顧客にWeb広告を配信したり、SEO記事を作成したりとさまざまなマーケティング戦略を考えることができます。

例えば決定木分析における決定ノードを「リピート購入の回数が3回以上」とし、Yesのブランチでつないだチャンスノードには「Z世代である」、Noでつないだチャンスノードには「高齢者である」といった形でパターン分けして記載しペルソナ像を特定していきます。

購入率の高いペルソナの条件を知ることで、より焦点を絞ったマーケティングができるため、売上アップにつながることが期待されます。

離脱とはWebマーケティング用語の1つで、Webサイトを訪問していたユーザーがそのサイトから離れることを意味します。

Webサイトの持ち主である企業は、サイトを訪問したターゲット顧客には商品やサービスの購入や問い合わせといった成果につながる行動を取ってほしいので、離脱率をなるべく下げたいと考えています。

この離脱につながる要素を特定したい場合にも決定木分析が役に立ちます。

例えば決定木分析における決定ノードを「離脱」とし、Yesのブランチでつないだチャンスノードには「年収400万円以上」、Noでつないだチャンスノードには「年収400万円未満」といった形で記載すると離脱するターゲット顧客のペルソナ像が特定可能です

下調べとしては次のようなデータを収集しておくとスムーズです。

• 離脱してしまった人へのアンケートやインタビューの結果（退会者アンケートなど）
• 顧客情報
• 顧客へのアンケートやインタビューの結果
• DMへの反応
• 問い合わせ履歴

離脱してしまうターゲット顧客のペルソナ像が特定できれば、マーケティング戦略として次にそのペルソナに対してどのようにアプローチをすればよいのかが考えやすくなります。

決定木分析のメリット

決定木分析を行うメリットを4つご紹介します。

必要な前処理が少ない

決定木分析においては、樹形図のブランチで分岐するYes、Noでデータを分類していくため、定性データの数値化や特徴量のスケーリングといった前処理を必要としません。

このことからデータ分析を行うにあたってかかる時間を大きく削減できることが期待されます。

結果の解釈が簡単にできる

決定木分析は統計学や数学が苦手な人でも結果の解釈がしやすい分析方法ですが、その理由には次のようなことが挙げられます。

• 樹形図を用いるため結果が一目見ればわかる
• ブランチとチャンスノードをたどれば分析の過程も含めて理解できる
• 樹形図全体がシンプルなレイアウトでできているため誰でも直感的に内容が理解できる

樹形図で整理した上で結果を提示するため、データの読み間違いなども起こりにくくなるでしょう。

汎用性が高い

データの分析手法は内容に応じて使い分ける必要があり、どのようなデータにも向いている分析手法というのは本来存在しないと考えてよいと言えます。

しかし決定木分析は仮定や制約が少ない分析手法のため、比較的汎用性が高くさまざまなデータを分析可能です。

前の項目でもご紹介したように、マーケティングだけではなく金融や医療など、分析を必要とするさまざまな場面で活用されているのはこの汎用性の高さから来るものです。

「仮定や制約が多い分析手法ほど汎用性が低くなる」と認識することが重要です。

膨大なデータを分析できる

例えば決定木分析なら同じアンケートの結果を分析するのでも、対象者や質問の数が少ない場合の調査結果から、対象者が幅広く質問の数も膨大な調査結果まで対応できます。

これは1つの樹形図上で複数のパターンを分析できるためですが、データ分析を効率良く進めたい際には大いに役立つと言えます。

決定木分析の注意点

決定木分析はメリットの大きい分析手法ですが、使用するにあたって注意しなければならない点を2つご紹介します。

分岐の数を適切に設定する

決定木分析を行う際に気をつけたいのがブランチとチャンスノードで作られる分岐と階層の深さです。分岐が少なすぎると階層も浅くなり、分析の精度が低くなります。

一方、分岐が多すぎると階層が深くなり、樹形図が複雑化してわかりにくいものになっていきます。

分岐が多すぎる状態を「過学習」と呼びますが、この状態ではあまり本質的ではないデータの誤差にまで適合した分析をしてしまうため、解釈がどんどん難しくなり分析の精度が低くなってしまいます。

このことから、決定木分析をする際は、「分岐の数を多くし過ぎずシンプルに維持する」と認識しておくことが大切です。

回帰分析と比べて精度が低い

決定木分析は確率的なアルゴリズムを使用するため、試算する期待値はあくまでも推定値であり、将来の正確な予測まではできません。

そのため精度だけで比較すると、回帰分析など他の手法の方が勝っている場合もあります。

決定木分析のメリットである結果のわかりやすさ、前処理の少なさ、汎用性の高さが活かせなければ他の手法でデータ分析をすることも検討してみてください。

まとめ

本記事では、決定木分析について解説しました。決定木分析とは、データを基に決定木と呼ばれる樹形図を作成し、分析を行う方法のことです。

この記事を参考にして、決定木分析をデータ分析にぜひ取り入れてみてください。

データ分析のサービス比較と企業一覧

AIsmiley編集部

株式会社アイスマイリーが運営するAIポータルメディア「AIsmiley」は、AIの専門家によるコンテンツ配信とプロダクト紹介を行うWebメディアです。AI資格を保有した編集部がDX推進の事例や人工知能ソリューションの活用方法、ニュース、トレンド情報を発信しています。

・Facebookでも発信しています
@AIsmiley.inc
・Xもフォローください
@AIsmiley_inc

メルマガに登録する